解决哪类问题需要使用HMM模型？HMM模型是什么？

什么样的问题解决可以用HMM模型。使用HMM模型时我们的问题一般有这两个特征：

1)我们的问题是基于序列的，比如时间序列，或者状态序列。

2)我们的问题中有两类数据，

一类序列数据是可以观测到的，即观测序列，而另一类数据是不能观察到的，即隐藏状态序列，简称状态序列。

有了这两个特征，那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。

比如：我现在给大家写课件，我在键盘上敲出来的一系列字符就是观测序列，而我实际想写的一段话就是隐藏状态。

序列，输入法的任务就是从敲入的一系列字符尽可能的猜测我要写的一段话，并把最可能的词语放在最前面让我选择，这就可以看做一个HMM模型了。

再举一个，假如我上课讲课，我发出的一串连续的声音就是观测序列，而我实际要表达的一段话就是隐藏状态序列，你大脑的任务，就是从这里串连续的声音中判断出我最可能要表达的话的内容。

从这些例子中，我们可以发现，HMM模型可以无处不在。但是上面的描述还不精确，下面我们用精确的数学符号来表述我们的HMM模型。

对于HMM模型，首先我们假设Q是所有可能的隐藏状态的集合，V是所有可能的观测状态的集合，即：

其中，N是可能的隐藏状态数，M是所有的可能的观察状态数。对于一个长度为T的序列，i是对应的状态序列, O是对应的观察序列，即：

HMM模型做了两个很重要的假设如下：

1) 齐次马尔科夫链假设。

即任意时刻的隐藏状态只依赖于它前⼀个隐藏状态。

当然这样假设有点极端，因为很多时候我们的某⼀个隐藏状态不仅仅只依赖于前⼀个隐藏状态，可能是前两个或者是前三个。

但是这样假设的好处就是模型简单，便于求解。

但是这样假设的好处就是模型简单，便于求解。如果在时刻t的隐藏状态是i = q ,在时刻t + 1的隐藏状态是i = q , 则从时刻t到时刻t+1的HMM状态转移概率。

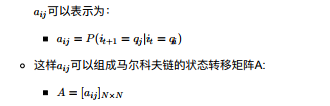
2） 观测独立性假设。即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态，这也是一个为了简化模型的假设。如果在时刻t的隐藏状态是i = q , 应对应的观察状态为o = v , 则该时刻观察状态v 在隐藏状态q 下生成的概率为b (k),满足：

一个HMM模型，可以由隐藏状态初始概率分布Π , 状态转移概率矩阵A和观测状态概率矩阵B决定。 Π ,A决定状态序列，B决定观测序列。因此，HMM模型可以由⼀个三元组λ 表示如下： λ = (A, B, Π) = (状态序列，观测序列，初始状态概率分布)